本文正體字版由OpenCC轉換

[二分圖帶權匹配與最佳匹配]

什麼是二分圖的帶權匹配？二分圖的帶權匹配就是求出一個匹配集合，使得集合中邊的權值之和最大或最小。而二分圖的最佳匹配則一定爲完備匹配，在此基礎上，纔要求匹配的邊權值之和最大或最小。二分圖的帶權匹配與最佳匹配不等價，也不互相包含。

我們可以使用KM算法實現求二分圖的最佳匹配。方法我不再贅述，可以參考tianyi的講解。KM算法可以實現爲O(N^3)。

[KM算法的幾種轉化]

KM算法是求最大權完備匹配，如果要求最小權完備匹配怎麼辦？方法很簡單，只需將所有的邊權值取其相反數，求最大權完備匹配，匹配的值再取相反數即可。

KM算法的運行要求是必須存在一個完備匹配，如果求一個最大權匹配(不一定完備)該如何辦？依然很簡單，把不存在的邊權值賦爲0。

KM算法求得的最大權匹配是邊權值和最大，如果我想要邊權之積最大，又怎樣轉化？還是不難辦到，每條邊權取自然對數，然後求最大和權匹配，求得的結果a再算出e^a就是最大積匹配。至於精度問題則沒有更好的辦法了。

[求最小(大)權匹配的費用流建模方法]

求最小(大)權匹配，可以用最小(大)費用最大流的方法。和二分圖最大匹配的構圖方法類似，添加附加源S和附加匯T，從S向二分圖X集合中每個頂點連接一條權值爲0，容量爲1的有向邊，從Y集合中每個頂點向T也連接一條權值爲0，容量爲1的有向邊。然後把原有的邊變成容量爲1，權值不變的有向邊。求從S到T的最小(大)費用最大流，就能求得最小(大)權匹配。

上述建模求最大權匹配的方法求得的一定是最佳匹配(如果存在完備匹配)，因爲S到X集合每條邊全部滿流。如下圖所示，最小費用最大流爲2。

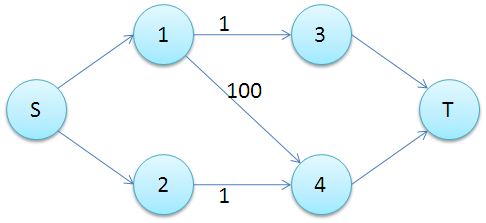
要求最大權匹配(不一定完備匹配)。如下圖，只需再引入一個頂點A，從X集合的每個頂點向A連接一條容量爲1，權值爲0的邊，然後再由A向T連接一條權值爲0，容量不小於|X|的邊，求最大費用最大流，這時是100。

最小權匹配也類似，不過新加的邊權要爲一個極大值，大於所有已有邊權值。

[KM算法與費用流的比較]

從理論上分析，KM算法的時間複雜度比費用流要好，但是實際上和較好的費用流算法比起來運行效率是差不多的，KM算法優勢僅僅在於編程容易。KM算法也有其不可避免的侷限性，就是必須用鄰接矩陣來表示。這樣會浪費很多的空間，尤其是圖相當稀疏的時候。而對於十分稀疏的圖，許多優秀的費用流算法效率是很高的。這並不說明KM算法不如費用流，畢竟在信息學競賽中，編程的複雜度也是一個相當重要的需要考慮的因素。

BYVoid 原創講解，轉載請註明。

上次修改時間 2017-05-22