本文正體字版由OpenCC轉換
問題簡述
對於0,1,…,N-1的N個整數,給定一個距離序列D0,D1,…,DN-1,定義一個變換序列T0,T1,…,TN-1使得每個i,Ti的環上距離等於Di。一個合法的變換序列應是0,1,…,N-1的一個排列,任務是要求出字典序最小的那個變換序列。
問題建模
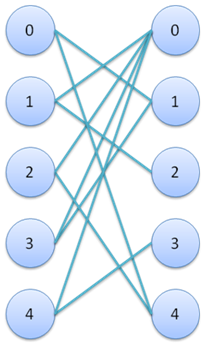
抽象成圖論模型,建立一個二分圖,X集合每個頂點代表0,1,…,N-1的N個整數,Y集合每個頂點爲對應的N個整數。X集合的第i個頂點向其環上距離爲Di的Y集合中的兩個頂點連一條邊。樣例建圖後如圖1所示。
圖 1
解法1 嘗試完美匹配
算法描述
顯然一個變換序列,就是二分圖的一個完美匹配,關鍵在於如何保證字典序最小。求字典序最小解得一般方法就是嘗試枚舉,並轉爲化判定性問題。於是方法就是,以此確定X集合每個頂點的對應點,首先嚐試讓其對應序號較小的頂點,然後判斷剩下的圖是否存在一個完美匹配(用匈牙利算法求最大匹配,判斷最大匹配數是否等於X集合剩餘頂點數)。如果存在,那麼當前頂點對應點就是序號較小的頂點,否則就是另一個頂點。最初應先判斷是否存在完美匹配,如果不存在,那麼該情況無解。
算法證明
假設還存在一個比當前方法求得的解T字典序更小的解V,那麼對於0<=i<=N-1一定有Vi<=Ti,並且存在一個j使得Vj<Tj。因爲Vj<Tj,所以X集合頂點j一定是對應的序號較大的頂點Tj,而Vj則是序號較小的頂點。由於如果j對應了Vj,剩餘的頂點不存在完美匹配,所以V不是合法解,因而不存在一個比當前方法求得的解T字典序更小的解V,T是字典序最小的解。複雜度分析
該圖的邊數是O(N)的,所以匈牙利算法的時間複雜度爲O(N2)。由於對於每個點都要進行一次匈牙利算法,所以該算法的時間複雜度爲O(N3)。在實際的測試數據中能拿到70分。參考程序
/*
* Problem: NOI2009 DAY1 transform
* Author: Guo Jiabao
* Time: 2009.7.27 10:20
* State: Done
* Memo: 二分圖匹配 + 暴力判斷
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int MAXN=20003,MAXM=MAXN*2;
struct edge
{
edge *next;
int t;
}*V[MAXN],ES[MAXM];
FILE *fi,*fo;
int N,EC;
int mat[MAXN],S[MAXN][2],T[MAXN];
bool vis[MAXN],lock[MAXN];
inline void addedge(int a,int b)
{
ES[++EC].next = V[a];
V[a] = ES+EC;
V[a]->t = b;
}
void init()
{
int i,t1,t2,d;
fi = fopen("transform.in","r");
fo = fopen("transform.out","w");
fscanf(fi,"%d",&N);
EC = 0;
for (i=1;i<=N;i++)
{
fscanf(fi,"%d",&d);
t1 = i + d;
if (t1>N) t1-=N;
t2 = i - d;
if (t2<1) t2+=N;
if (t1 < t2)
S[i][0] = t1,S[i][1] = t2;
else
S[i][0] = t2,S[i][1] = t1;
addedge(i,S[i][1]+N);
addedge(i,S[i][0]+N);
}
}
bool aug(int i)
{
for (edge *e=V[i];e;e=e->next)
{
int j = e->t;
if (!vis[j] && !lock[j])
{
vis[j] = true;
if (!mat[j] || aug(mat[j]))
{
mat[j] = i;
return true;
}
}
}
return false;
}
bool hungary()
{
memset(mat,0,sizeof(mat));
for (int i=1;i<=N;i++)
{
if (lock[i]) continue;
memset(vis,0,sizeof(vis));
if (!aug(i))
return false;
}
return true;
}
bool solve()
{
int i,j;
if (!hungary())
return false;
for (i=1;i<=N;i++)
{
lock[i] = true;
for (j=0;j<=1;j++)
{
if (!lock[S[i][j]+N])
{
lock[S[i][j]+N] = true;
if (hungary())
{
T[i] = S[i][j];
break;
}
lock[S[i][j]+N] = false;
}
}
}
return true;
}
void print(bool win)
{
if (win)
{
int i;
for (i=1;i<N;i++)
fprintf(fo,"%d ",T[i] - 1);
fprintf(fo,"%d\n",T[i] - 1);
}
else
fprintf(fo,"No Answer\n");
fclose(fi);
fclose(fo);
}
int main()
{
init();
print(solve());
return 0;
}
解法2 調整匹配
算法描述
首先求一個任意完美匹配,然後在此基礎上,不斷尋找增廣迴路,以改進當前解,直到最優解。具體方法爲,依次斷每個頂點的對應。如果當前頂點對應的點是序號較小頂點,可以直接取得,否則嘗試修正。修正的方法是強制將當前頂點對應到序號較小頂點,這必然導致X集合中另一個頂點失配,此時從該頂點開始嘗試找一條增廣路,如果存在則修正成功,否則修正失敗,撤回操作。
算法證明
證明類似與解法1,不同在於每次無重新判斷,只要修正保證合法,每時總是完美匹配。複雜度分析
首先求一個完美匹配的時間複雜度爲O(N2),接下來要嘗試修正N次,每次修正時時間爲O(N),所以總時間複雜度爲O(N2)。由於算法常數較小,在實際的測試數據中拿到了100分。
參考程序
/*
* Problem: NOI2009 transform
* Author: Guo Jiabao
* Time: 2009.9.17 15:10
* State: Solved
* Memo: 二分圖匹配 + 修正
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;
const int MAXN=20001,MAXM=MAXN*4;
struct edge
{
edge *next;
int t;
}*V[MAXN],ES[MAXM];
int N,EC,Current;
int S[MAXN][2],mat[MAXN];
bool vis[MAXN];
inline void addedge(int a,int b)
{
ES[++EC].next = V[a]; V[a] = ES + EC;
V[a]->t = b;
}
void init()
{
freopen("transform.in","r",stdin);
freopen("transform.out","w",stdout);
scanf("%d",&N);
int i,d,t1,t2;
for (i=1;i<=N;i++)
{
scanf("%d",&d);
t1 = i + d;
if (t1>N) t1-=N;
t2 = i - d;
if (t2<1) t2+=N;
if (t1 < t2)
S[i][0] = t1,S[i][1] = t2;
else
S[i][0] = t2,S[i][1] = t1;
addedge(i,S[i][0]+=N);
addedge(i,S[i][1]+=N);
}
}
bool augment(int i)
{
if (i <= Current)
return false;
for (edge *e=V[i];e;e=e->next)
{
int j = e->t;
if (!vis[j])
{
vis[j] = true;
if (!mat[j] || augment(mat[j]))
{
mat[j] = i;
mat[i] = j;
return true;
}
}
}
return false;
}
void hungary()
{
Current = 0;
int cnt = 0;
for (int i=1;i<=N;i++)
{
memset(vis,0,sizeof(vis));
if (augment(i))
cnt++;
}
if (cnt < N)
{
printf("No Answer\n");
exit(0);
}
}
void fix()
{
for (int i=1;i<=N;i++)
{
if (mat[i] != S[i][0])
{
Current = i;
memset(vis,0,sizeof(vis));
int t = mat[ S[i][0] ];
mat[ S[i][1] ] = 0;
mat[ S[i][0] ] = i;
vis[ S[i][0] ] = true;
if (augment(t))
{
mat[i] = S[i][0];
}
else
{
mat[ S[i][1] ] = i;
mat[ S[i][0] ] = t;
}
}
}
}
void solve()
{
hungary();
fix();
}
void print()
{
int i;
for (i=1;i<N;i++)
printf("%d ",mat[i] - N - 1);
printf("%d\n",mat[i] - N - 1);
}
int main()
{
init();
solve();
print();
return 0;
}
解法3 倒序匹配
算法描述
這個方法很神奇,只用求一次完美匹配,要從X集合最後一個頂點到第一個頂點的順序求每個頂點出發的增廣路,求增廣路的過程中應優先選擇序號較小點。算法證明
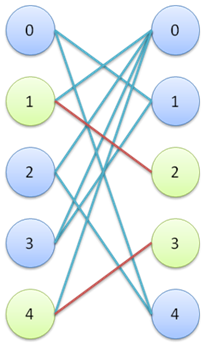
實現簡單的方法往往證明並不容易,該算法運用了貪心的思想。首先我們可以發現,有一些可以直接確定的匹配,這些就是度爲1的頂點,必須與其唯一的對應點對應。樣例如圖2所示,(1,2),(4,3)一定存在於任意一個解中(如果有解的話)。這樣的話,我們就可以把已經確定的頂點去除,刪除後如果又發現了剩餘度爲1的頂點,那麼繼續去除,直到不存在爲止。圖 2
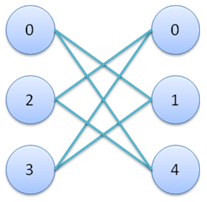
剩下的頂點中,X集合頂點個數一定與Y集合頂點個數相等。X集合每個頂點的度都是2,所以Y集合中的所有頂點度也都是2。於是剩下的頂點構成了若干個互不連同的環,每個頂點屬於且只屬於一個環,我們只需在此圖上求字典序最小的匹配即可。每個環的匹配只有兩種方式,如果我們從環上X集合中序號最小的頂點貪心的選擇與序號較小的點匹配,那麼該環上的匹配就是字典序最小。樣例如圖3。
圖 3
由於事先不知道那些頂點在環上,哪些可以直接確定。從X集合每個頂點倒序查找增廣路,就可以保證最後的最優,也就是字典序儘量小。因爲如果一個頂點在環上,找到的一定是環上較優的匹配方式,而不在環上的點也可以被後來的增廣而修正。
複雜度分析
求一次完美匹配的時間複雜度爲O(N2),在實際的測試數據中拿到了100分。參考程序
/*
* Problem: NOI2009 transform
* Author: Guo Jiabao
* Time: 2009.9.17 15:29
* State: Solved
* Memo: 二分圖匹配
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;
const int MAXN=20001,MAXM=MAXN*4;
struct edge
{
edge *next;
int t;
}*V[MAXN],ES[MAXM];
int N,EC;
int S[MAXN][2],mat[MAXN];
bool vis[MAXN];
inline void addedge(int a,int b)
{
ES[++EC].next = V[a]; V[a] = ES + EC;
V[a]->t = b;
}
void init()
{
freopen("transform.in","r",stdin);
freopen("transform.out","w",stdout);
scanf("%d",&N);
int i,d,t1,t2;
for (i=1;i<=N;i++)
{
scanf("%d",&d);
t1 = i + d;
if (t1>N) t1-=N;
t2 = i - d;
if (t2<1) t2+=N;
if (t1 < t2)
S[i][0] = t1,S[i][1] = t2;
else
S[i][0] = t2,S[i][1] = t1;
addedge(i,S[i][1]+=N);
addedge(i,S[i][0]+=N);
}
}
bool augment(int i)
{
for (edge *e=V[i];e;e=e->next)
{
int j = e->t;
if (!vis[j])
{
vis[j] = true;
if (!mat[j] || augment(mat[j]))
{
mat[j] = i;
mat[i] = j;
return true;
}
}
}
return false;
}
void solve()
{
int cnt = 0;
for (int i=N;i>=1;i--)
{
memset(vis,0,sizeof(vis));
if (augment(i))
cnt++;
}
if (cnt < N)
{
printf("No Answer\n");
exit(0);
}
}
void print()
{
int i;
for (i=1;i<N;i++)
printf("%d ",mat[i] - N - 1);
printf("%d\n",mat[i] - N - 1);
}
int main()
{
init();
solve();
print();
return 0;
}
解法4 貪心
算法描述
按照解法3證明中的描述,我們可以預處理所有已經確定的匹配,並在圖中刪去。對於剩下的每個環,只需從序號最小的點開始深度優先搜索,並進行匹配即可。算法證明
證明同解法3。複雜度分析
預處理的時間複雜度爲O(N),深度優先搜索的時間複雜度爲O(N),所以總時間複雜度爲O(N)。在實際的測試數據中拿到了100分。參考程序
```cpp /* * Problem: NOI2009 transform * Author: Guo Jiabao * Time: 2009.9.17 18:37 * State: Solved * Memo: 貪心 */ #includestruct edge { edge *next; int t; }*V[MAXN],ES[MAXM];
int N,EC,Stack[MAXN]; int S[MAXN][2],deg[MAXN],mat[MAXN]; bool nuked[MAXN];
inline void addedge(int a,int b) { ES[++EC].next = V[a]; V[a] = ES + EC; V[a]->t = b; ES[++EC].next = V[b]; V[b] = ES + EC; V[b]->t = a; ++deg[b]; mat[b] = a; }
void init() { freopen(“transform.in”,“r”,stdin); freopen(“transform.out”,“w”,stdout); scanf("%d",&N); int i,d,t1,t2; for (i=1;i<=N;++i) { scanf("%d",&d); t1 = i + d; if (t1>N) t1-=N; t2 = i - d; if (t2<1) t2+=N; if (t1 < t2) S[i][0] = t1,S[i][1] = t2; else S[i][0] = t2,S[i][1] = t1; addedge(i,S[i][1]+=N); addedge(i,S[i][0]+=N); deg[i] = 2; } }
inline void Match(int i,int j) { mat[i] = j; mat[j] = i; }
void dfsMatch(int i,bool s) { nuked[i] = true; int j; for (edge *e=V[i];e;e=e->next) { j = e->t; if (!nuked[j]) { dfsMatch(j,!s); if (s) Match(i,j); break; } } }
void noAnswer() { printf(“No Answer\n”); exit(0); }
void cut() { int Stop = 0,i,j; for (i=1;i<=N;++i) { if (deg[i+N] == 0) noAnswer(); else if (deg[i+N] == 1) Stack[++Stop] = i+N; } while (Stop) { i = Stack[Stop–]; nuked[i] = true; for (edge *e=V[i];e;e=e->next) { j = e->t; if (!nuked[j]) break; } Match(i,j); i = j; nuked[i] = true; for (edge *e=V[i];e;e=e->next) { j = e->t; if (!nuked[j]) { deg[j]–; if (deg[j] == 0) noAnswer(); else if (deg[j] == 1) Stack[++Stop] = j; } } } }
void solve() { cut(); for (int i=1;i<=N;i++) { if (!nuked[i]) { dfsMatch(i,true); } } }
void print() { int i; for (i=1;i<N;i++) printf("%d “,mat[i] - N - 1); printf("%d\n”,mat[i] - N - 1); }
int main() { init(); solve(); print(); return 0; }
上次修改時間 2017-05-26