本文正體字版由OpenCC轉換
問題簡述
能量場中有N個粒子,每個粒子都有一個質量m和結合係數c,兩個粒子a,b合併時會產生mamb(ca - cb)的能量。(1)找出兩個粒子相結合,使得產生的能量最大。(2)從中找出任意k個粒子排列成一個環,相鄰兩個粒子分別合併,使得總能量最大,產生負能量的粒子必須是環上連續的一段。
問題分析
乍一看這個問題的第一問好像很簡單,枚舉每對粒子即可,但是時間複雜度是O(N2)的,而且難以想到如何優化。第二問則更加困難,搜索、動態規劃是肯定不行的,貪心、圖論也難以找到建模方式。分析發現這個問題可以歸約到一個0/1規劃問題,如果沒有特殊性將無法解決,而特殊性無非在於能量產生的公式,因此將目光聚焦到這個公式上,對公式進行一些變形:
- mamb(ca - cb)
- = mambca - mambcb
- = macamb - mbcbma
- 設xi=mici,yi=mi則原式
- = xa*yb - xb*ya
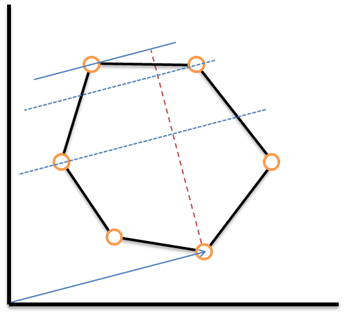
經過變形,我們可以明顯地看出公式變形爲了兩個向量叉積的公式,這給我們以啓發:把每個粒子看做平面上的一個點,兩個粒子合併產生的能量就是原點指向兩個點的向量的叉積。因此問題的第一問就轉化爲了:找到兩個向量,使它們的叉積最大。而第二問找到一個環合併的公式恰好對應了多邊形的面積公式,再加上“產生負能量的粒子必須是環上連續的一段”這個限制,這個多邊形必須是簡單多邊形[1]。
要使第二問要求的環對應的多邊形面積儘量大,應是平面上這些點能組成的最大的簡單多邊形,那麼就應該是這些點的凸包。
相較之下第一問反而更難求解,不過有了對應的幾何意義,就容易下手了。兩個向量的叉積對應了兩個向量所夾的平行四邊形的有向面積,要使之最大首先應該是正值,即讓第一個向量在第二個向量順時針方向。當我們確定了第一個向量[2],即確定了平行四邊形的一個底邊,要使面積最大,應最大化平行四邊形的高。於是我們可以做一條與該向量平行的直線,不斷向上平移,直到遇到距離最遠的點爲止,這樣的高最大。第一個向量與這個最遠的點對應的向量做叉積就是對應的最大面積,很顯然這個最遠的點一定在凸包上,反過來考慮第一個向量的終點也一定在凸包上,因此查找這對向量時只需考慮凸包上的點。
有這個性質以後,如果直接枚舉這對頂點,可能會快不少,但時間複雜度依然是O(N2)的。這時如果我們以某種特定的順序枚舉第一個向量,可以減少不少枚舉量。具體方法是將從原點到凸包上所有的點的向量按照逆時針方向排序,按順序枚舉,這時候我們枚舉的向量就是逆時針方向移動的,對應的第二個向量的終點在凸包上也是逆時針順序移動(從最上點到最左點),因此枚舉就是均攤線性的時間複雜度了。
算法描述
-
將所有粒子抽象爲平面第一象限內的一個點(mici,mi)。
-
求平面上點的凸包。
-
把凸包上的點按照向量極角的順序排序依次枚舉作爲第一個向量i。
-
找到對應第二個向量的終點j,應滿足向量<j,j+1>在向量i逆時針方向。
複雜度分析
求凸包的時間複雜度爲O(NlogN),枚舉最優向量對的時間複雜度爲O(N),因此總體時間複雜度爲O(NlogN)。
參考程序
/*
* Problem: NOI Winter Camp 2010 efield
* Author: Guo Jiabao
* Time: 2010.3.15 12:21
* Label: Solved
* Memo: Computing Geometry + Convex Hull + Graham Scan
*/
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <iostream>
#include <sstream>
#include <vector>
#include <list>
#include <deque>
#include <string>
#include <queue>
#define var(a,b) typeof(b) a(b)
#define foreach(a,b) for (var(a,b.begin());a!=b.end();++a)
using std::sort;
const int MAXN = 50002;
struct point
{
double x,y;
int id;
};
int N,ipole;
point P[MAXN],pole,convex[MAXN],A[MAXN];
point operator -(const point &a,const point &b)
{
point t={a.x-b.x,a.y-b.y,0};
return t;
}
double operator *(const point &a,const point &b)
{
return a.x*b.y - b.x*a.y;
}
void init()
{
freopen("efield.in","r",stdin);
freopen("efield.out","w",stdout);
scanf("%d",&N);
ipole=0;
for (int i=1;i<=N;i++)
{
double m,c;
scanf("%lf%lf",&m,&c);
P[i].x = m*c;
P[i].y = m;
P[i].id = i;
if (P[i].y > P[ipole].y)
ipole = i;
}
pole = P[ipole];
P[ipole] = P[N--];
}
bool cmp(const point &a,const point &b)
{
point p = a - pole;
point q = b - pole;
double fc = p * q;
if (fc > 0)
return true;
if (fc < 0)
return false;
return (p.x * p.x + p.y * p.y > q.x * q.x + q.y * q.y);
}
void graham()
{
int top;
sort(&P[1],&P[N+1],cmp);
convex[1] = pole;
convex[top=2] = P[1];
for (int i=2;i<=N;i++)
{
point p = convex[top] - convex[top-1];
point q = P[i] - convex[top];
if (p*q < 0)
{
top--;
i--;
}
else
convex[++top] = P[i];
}
N = top;
convex[N+1] = convex[1];
}
void getSumArea()
{
int i;
printf("%d\n",N);
for (i=1;i<N;i++)
printf("%d ",convex[i].id);
printf("%d\n",convex[i].id);
/* double SumArea = 0;
for (i=1;i<=N;i++)
SumArea += convex[i] * convex[i+1];
SumArea *= 0.5;*/
}
bool cmp2(const point &a,const point &b)
{
return a * b > 0;
}
void getPair()
{
int M = 1,i,j,ai,aj;
double PairArea = 0;
for (i=1;i<=N;i++)
{
A[i] = convex[i];
if (convex[i].x < convex[i-1].x)
M = i;
}
sort(&A[1],&A[N+1],cmp2);
for (i=1,j=1;i<=N;i++)
{
while (j<M && A[i]*(convex[j]-convex[j+1]) <= 0)
j++;
if (j == M)
break;
double cur = A[i] * convex[j];
if (cur > PairArea)
{
PairArea = cur;
ai = A[i].id;
aj = convex[j].id;
}
}
printf("%d %d\n",ai,aj);
}
void solve()
{
graham();
getPair();
getSumArea();
}
int main()
{
init();
solve();
return 0;
}
</>[1] 如果不是簡單多邊形,則面積公式一定會有多段連續的負值。
[2] 即順時針方向下方的那個向量,下同。
附錄
本題答案不唯一,因此需要一個Special Judge,我寫了一個Cena的。使用方法就是編譯後放進數據文件夾,添加題目的時候設置自定義校驗器,如果實在不會看幫助吧。
下載地址:efield-check-cena.zip
上次修改時間 2017-05-26